Abstract
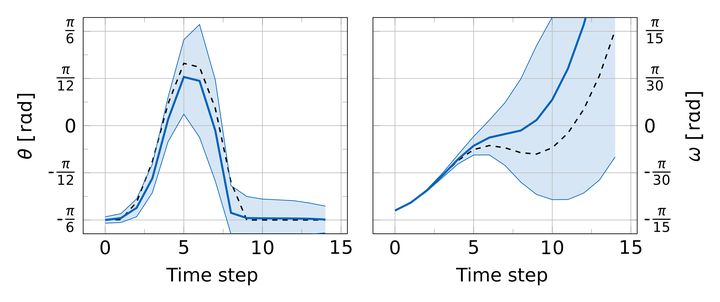
In reinforcement learning, an agent has to learn how to make decisions in an unknown environment in order to maximize a numerical reward. In model-based reinforcement learning, the experience gained via interaction is represented as a transition model which can be used to simulate the system’s future behaviour. This thesis is concerned with reducing the model bias introduced by choosing actions which are optimal with respect to an imperfect model. Instead of relying on a single deterministic model, gathered knowledge is represented using Gaussian processes which encode a probability distribution over all plausible transition models. By averaging over all of them, the expected long-term reward is calculated, which explicitly incorporates model uncertainties into long-term planning. A controller is formulated by applying Particle Swarm Optimization to this expected reward, directly choosing appropriate actions. Besides formally introducing these tools, this thesis investigates their effectiveness on a benchmark problem with the task of learning how to balance and navigate a bicycle. Thereby, multiple approaches of incorporating uncertainties are described and compared to the classic technique of deterministic predictions.
Markus Kaiser
Research Scientist
Research Associate at the University of Cambridge and Research Scientist at Siemens AG. I am interested in scalable Bayesian machine learning and Gaussian processes.