Abstract
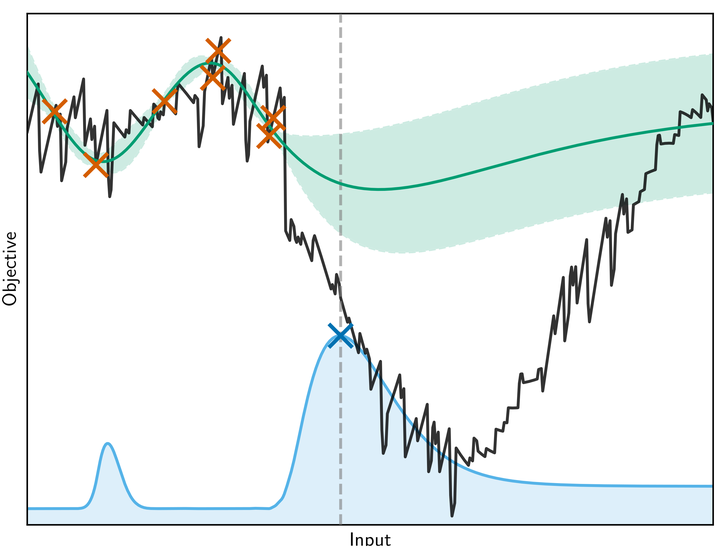
We present an approach to Bayesian Optimization that allows for robust search strategies over a large class of challenging functions. Our method is motivated by the belief that the trends useful to exploit in search of the optimum typically are a subset of the characteristics of the true objective function. At the core of our approach is the use of a Latent Gaussian Process Regression model that allows us to modulate the input domain with an orthogonal latent space. Using this latent space we can encapsulate local information about each observed data point that can be used to guide the search problem. We show experimentally that our method can be used to significantly improve performance on challenging benchmarks.
Type
Publication
ICML