Abstract
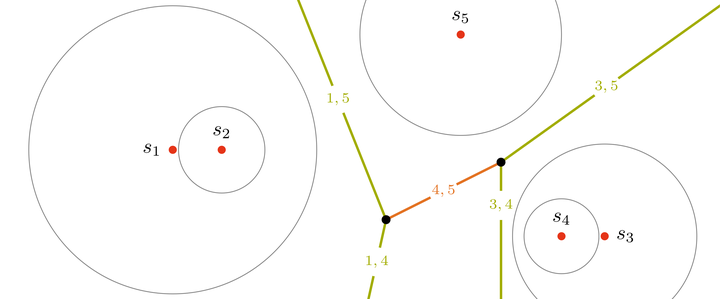
Power diagrams are a generalization of Voronoi diagrams which define a cell decomposition of an euclidean space based on a finite set of spheres, assigning every sphere a polyhedral cell for which it minimizes the power function of the points with respect to all spheres. This interdisciplinary project is concerned with the implementation of an algorithm that yields the incidence structure of such a diagram. First, power diagrams are introduced and some fundamental results provided. It continues with the investigation of the close relationship of power diagrams in $d$ dimensions to arrangements of hyperplanes in $d+1$ dimensions and the convex hull of points obtained via their polarization. This connection gives rise to an efficient algorithm for computing power diagrams, for which both a formal definition and the description of an implementation is presented.
Markus Kaiser
Research Scientist
Research Associate at the University of Cambridge and Research Scientist at Siemens AG. I am interested in scalable Bayesian machine learning and Gaussian processes.